Why FROST?
In order to improve efficiency of Coinbase’s threshold-signing systems, we decided to explore the FROST threshold Schnorr signature protocol, which features the following advantages over other Schnorr-based threshold signature protocols [GJKR03, SS01]:
Low round complexity in both the distributed key-generation and signing phases. The distributed key generation phase can be completed in 2 rounds. The signing phase can be completed in less or equal to 3 rounds depending on whether we use a signature aggregator role and a preprocessing stage. That is,
1-round signing with a trusted signature aggregator and a preprocessing stage.
2-round signing with a trusted signature aggregator, but no preprocessing stage.
3-round signing without a trusted signature aggregator and no preprocessing stage.
Concurrent security. The signing phase is secure when performed concurrently. That is, an unlimited number of signature operations can be performed in parallel. In contrast with other threshold Schnorr signature protocols, there are existing Schnorr-based threshold signature protocols, such as [GJKR03, SS01], that have the same round complexity, but they suffer from limited concurrency to protect against the attack of Drijvers et al. [ DEF19]. This attack was originally proposed in a Schnorr multi-signature n-out-of- n setting, but it also applies similarly in a threshold t-out-of- n setting with the same parameters for an adversary that controls up to t-1 participants. We refer readers to section 2.6 of the FROST draft for more details. To prevent this attack without limiting concurrency, FROST binds each participant’s response to a specific message as well as the set of participants and their set of elliptic curve (EC) points used for that particular signing operation. In doing so, combining responses over different messages or EC point pairs results in an invalid signature, thwarting attacks such as those of Drijvers, et al.
Secure against dishonest majority. FROST is secure against adversaries which control up to t-1 signers in the signing phase.
Simple cryptographic building blocks and assumptions. FROST is built upon the threshold Shamir secret sharing and Feldman verifiable secret sharing schemes and it relies only on the discrete logarithm assumption.
How does FROST work?
Before we introduce how FROST works, we first recall how the standalone Schnorr signature works.
A Schnorr digital signature algorithm is a triple of algorithms: (KeyGen, Sign, Verify).
Let G be a group generator of a cyclic group with prime order p, and let H be a cryptographic hash function mapping to the field Z ₚ *. A Schnorr signature is generated over a message m by the following steps:
KeyGen -> (sk, vk)
Randomly sample the secret key sk <- Z ₚ.
Return (sk, vk = sk * G).
Sign(sk, m) -> sig
Randomly sample a secret nonce k <- Z ₚ.
R = k * G
c = H(m, R)
z = k + sk * c (mod p)
Return signature sig = (z, c)
Verify(vk, m, sig) -> true/false
Parse sig = (z’, c’)
R’ = z * G -c * vk
c’ = H(m, R’)
Return true if c = c’, otherwise return false.
We call (sk, vk) the secret and verification keys respectively. We call m the message being signed and sig the Schnorr digital signature.
FROST is a threshold Schnorr signature protocol that contains two important components. First, n participants run a distributed key generation (DKG) protocol to generate a common verification key; at the end, each participant obtains a private secret key share and a public verification key share. Afterwards, any t-out-of-n participants can run a threshold signing protocol to collaboratively generate a valid Schnorr signature. The figure below gives a high-level sketch of how FROST works in the case of t = 3 and n = 5.
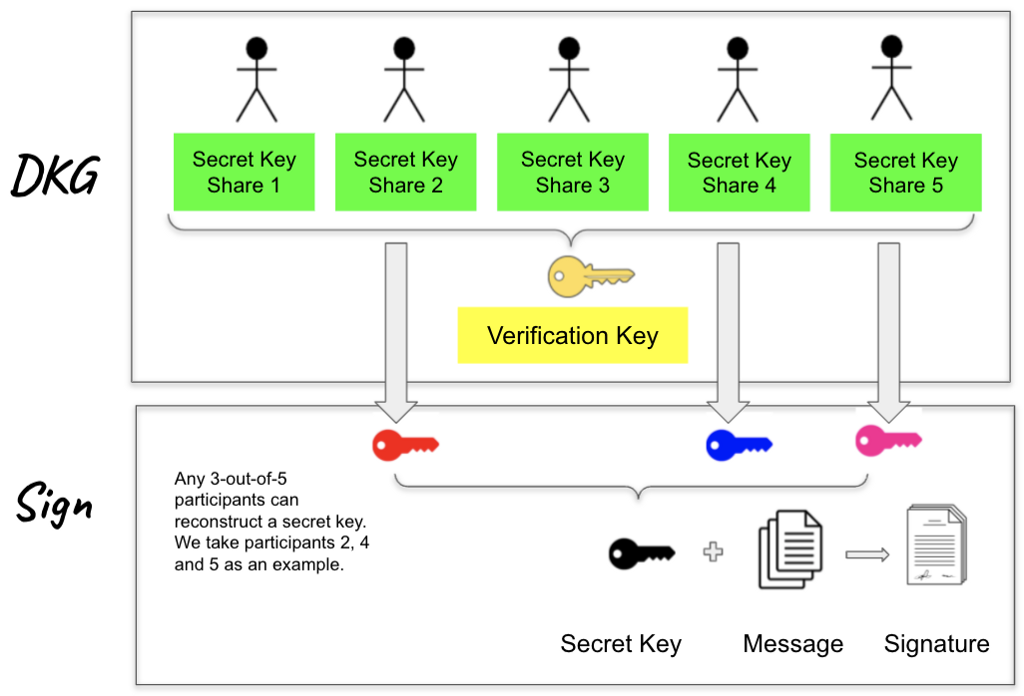
In the following context, we introduce FROST distributed key generation and threshold signing in more technical details.
FROST — distributed key generation (DKG). The secret signing key in Schnorr signature is an element in the field Z ₚ. The goal of this phase is to generate long-lived secret key shares and a joint verification key. This phase is run by n participants. FROST builds its own key generation phase upon Pedersen’s DKG [ GJKR03], in which it uses both Shamir secret sharing and Feldman’s verifiable secret sharing schemes as subroutines. In addition, FROST also requires each participant to demonstrate knowledge of their own secret by sending to other participants a zero-knowledge proof, which itself is a Schnorr signature. This additional step protects against rogue-key attacks in the setting where t ≥ n/2.
At the end of the DKG protocol, a joint verification key vk is generated. Also, each participant P ᵢ holds a value (i, sk ᵢ ) that is their long-lived secret share and a verification key share vk ᵢ = sk ᵢ *G. Participant P ᵢ’s verification key share vk ᵢis used by other participants to verify the correctness of P ᵢ’s signature shares in the signing phase, while the verification key vk is used by external parties to verify signatures issued by the group.
FROST — threshold signing. We now introduce the signing protocol for FROST. This phase builds upon known techniques that employ additive secret sharing and share conversion to non-interactively generate the nonce for each signature. This phase also leverages binding techniques to avoid known forgery attacks without limiting concurrency.
Our implementation is slightly adapted from the FROST draft. In our implementation, we opted to not use the signature aggregator role. Instead, each participant is a signature aggregator. This design is more secure: all the participants of the protocol verify what others have computed to achieve a higher level of security and reduce risk. In contrast with other open source libraries, as far as we know, we are the first to implement FROST without the signature aggregator role. Furthermore, we have chosen not to do the (one-time) preprocessing stage in order to speed up the implementation. In the preprocessing stage, each participant prepares a fixed number of EC point pairs for further use, which is run for a single time for multiple threshold signing phases. However, we take this stage as an additional round and only prepare a single pair of EC points, which means we run it every time for each threshold signing phase. In more detail, there are two major differences between our implementation and the original draft.
First, the signature aggregator, as described in the draft, validates messages that are broadcast by cosigners and computes the final signature. In our implementation, we do not use such a role. Instead, each participant simply performs a broadcast in place of a signature aggregator performing coordination. Note that FROST can be instantiated without such a signature aggregator as stressed in the draft. Also, implementing it in a decentralized way is more appropriate to Coinbase’s multiparty computation approach.
Second, the protocol in the draft uses a preprocessing stage prior to signing, where each participant P ᵢ samples a sequence number, say Q, of single-use nonces (d ᵢⱼ , e ᵢⱼ ), computes and broadcasts pairs of public points (D ᵢⱼ = d ᵢⱼ *G, E ᵢⱼ = e ᵢⱼ *G) for further use in subsequent signing rounds, where j = 1….Q. This preprocessing stage is a once-for-all stage. That is, each participant can prepare a fixed number of EC point pairs, say Q, and broadcast them to the signature aggregator, then the signature aggregator distributes these EC point pairs to all participants for further use. Once these pairs of EC points are used up, then these participants should run another preprocessing stage. Since we opted to not use such a signature aggregator role in our implementation, we have chosen instead to let each participant generate a single pair of EC points (D ᵢ , E ᵢ ). Therefore, there is no preprocessing stage in our implementation and thus there are 3 rounds in our threshold signing phase instead of 2. Also note that whether our implementation contains the preprocessing stage or not simply depends on how many EC point pairs are generated in signing round 1. If each participant generates a Q number of EC point pairs in the signing round 1, then this round can be viewed as the preprocessing stage and our implementation becomes a 2-round signing protocol.
We describe how these three signing rounds work and give some technical details.
Signing Round 1. Each participant P ᵢ begins by generating a single private nonce pair (d ᵢ , e ᵢ ) and corresponding pair of EC points (D ᵢ , E ᵢ ) and broadcasts this pair of points to all other participants. Each participant stores these pairs of EC points received for use later. Signing rounds 2 and 3 are the actual operations in which t-out-of-n participants cooperate to create a valid Schnorr signature.
Signing Round 2. To create a valid Schnorr signature, any t participants work together to execute this round. The core technique behind this round is t-out-of-t additive secret sharing. This technique creates the secret nonce k = SUM(k ᵢ ), which is the same value generated in the single-party Schnorr signing algorithm, and each k ᵢ is the share computed by participant P ᵢ. To do this, each participant prepares the set of pairs of EC points B = (D ₁ , E ₁ )……(D ₜ , E ₜ ) received in round 1, and then computes k ᵢ = d ᵢ +e ᵢ *r ᵢ , where r ᵢ =H(i, m, B) and H is a hash function whose outputs are in the field Z ₚ. Computing r ᵢ is important since it works as a binding value for each participant to prevent the forgery attack. Then each participant computes the commitment R ᵢ =D ᵢ +E ᵢ *r ᵢ such that it binds the message m, the set of signing participants and each participant’s EC points to each signature share, such that signature shares for one message cannot be used for another. This prevents the forgery attack because attackers cannot combine signature shares across distinct signing operations or permute the set of signers or published points for each signer. The commitment for the set of signers is then simply R = SUM(R ᵢ ). As in single-party Schnorr signatures, each participant computes the challenge c = H(m, R).
Having computed the challenge c, each participant is able to compute the response z ᵢ to the challenge using the single-use nonces (d ᵢ , e ᵢ ) and the long-term secret shares sk ᵢ, which are t-out-of-n (degree t-1) Shamir secret shares of the group’s long-lived key sk. One main observation that FROST leverages is that if k ᵢ are additive shares of k, then each k ᵢ /L ᵢ are t-out-of-n Shamir shares of k, where L ᵢ is the Lagrange coefficient for participant P ᵢ. That is, L ᵢ = prod(i/(j-i)), where j = 1,…,t, j ≠i. This observation is due to the work by Benaloh and Leichter [ BL88] and the work by Cramer, Damgaard and Ishai [ CDI05]. They present a non-interactive mechanism for participants to locally convert additive shares generated via the Benaloh and Leichter t-out-of-n secret sharing construction to Shamir’s polynomial form. FROST uses the simplest t-out-of-t case of this transformation. Thus k ᵢ /L ᵢ +sk ᵢ *c are degree t-1 Shamir secret shares of the correct response z = k+sk*c for a plain (single-party) Schnorr signature. Using share conversion again and the value each participant has computed (namely, k ᵢ = d ᵢ +e ᵢ *r ᵢ), we get that z ᵢ =d ᵢ +e ᵢ *r ᵢ +L ᵢ *sk ᵢ *c are t-out-of-t additive shares of z. At the end of signing round 2, each participant broadcasts z ᵢ to other participants.
Signing Round 3. After receiving z ᵢ from all other participants, each participant checks the consistency of these reported z ᵢ, with their pair of EC points (D ᵢ , E ᵢ ) and their verification key share vk ᵢ. This can be done by checking the equation z ᵢ *G = R ᵢ +c*L ᵢ *vk ᵢ. Once all z ᵢ are valid, then each participant computes z = SUM(z ᵢ ) and output (z, c) as the final Schnorr signature. This signature will verify properly to any party unaware that FROST was used to generate the signature, and can check it with the standard single-party Schnorr verification equation with vk as the verification key. As we have mentioned, we do not use the signature aggregator role in our implementation. Thus, each participant works as a signature aggregator. Therefore, we let each participant self-verify its own signature before outputting it.
Implementation Challenges
We referred to some known FROST implementations: two Rust implementations — one by ZCash foundation and another by frost-dalek— but they are not appropriate to our tech stack. One Golang implementation is from the Taurus group, but unfortunately this Go implementation is not ready for production use and has not been externally audited. As a result, we decided to implement the protocol in-house.
One feature of FROST signing is that each participant must know Lagrange coefficients for each participant in order to compute z ᵢ. This is uncommon in other threshold signature protocols that use Feldman verifiable secret sharing as a sub-protocol, so there are few existing Go libraries to support THIS. Most existing libraries support generating secret shares, polynomials, and their interpolation, but do not support Lagrange coefficient computation. To fill in this technical gap, we implemented participants’ Lagrange coefficients given arbitrary t participant IDs as input. Before running the threshold signing protocol, it takes input IDs of the t participants and generates all Lagrange coefficients. As the FROST draft suggests, we assign these coefficients to each participant before signing to improve performance.
Summary
FROST is a flexible, round-optimized Schnorr threshold signature scheme that minimizes the network overhead of producing Schnorr signatures in a threshold setting while allowing for unrestricted parallelism of signing operations and only a threshold number of signing participants. We introduce FROST, highlight its features, and describe it in a fully decentralized approach (i.e., without any third-party signature aggregator). This post exposes what Coinbase discovered while evaluating and implementing the FROST protocol and we look forward to adding it to our suite of threshold signing services.
If you are interested in cutting-edge cryptography, Coinbase is hiring.
was originally published in The Coinbase Blog on Medium, where people are continuing the conversation by highlighting and responding to this story.